From the perspective of this blog, the most important advance provided by the Relativistic Transactional Interpretation (RTI, [1]) of quantum physics is the replacement of the ad hoc Born Rule with a physical process and freeing from its ties to measurement. This process involves an interplay between the quantum substrate (QS) and the space-time layer of empirical events, as discussed previously. Not only are there empirical events in space-time (constructed from past events) but also non-empirical QS events outside space-time. As shown in the previous post, the quantum state changes from that obtained through unitary propagation to a state associated with the projection on to the space-time event due to conditioning on that projection. So, there is an observable stochastic process in space-time and a hidden (not observable) QS stochastic process governed by the same transition probabilities. This interplay between the QS and space-time events needs further discussion.
Ruth Kastner explains in detail [1] how RTI quantum theory developed from the classical Wheeler-Feynman Absorber Theory of Radiation [2, 3]. In chapter 5 she reaches the technical core of the book that builds on the quantum adaptation of absorber theory by Davies [4,5]. The historical progression will not be our concern here but the formal structure of the argument. In the book two further references are provided and they help in presenting the structure. They are a joint paper with John Cramer [6] and a paper explicitly on the measurement problem [7].
It is a theme of this blog that events in the micro-domain cannot be restricted to measurements so the argument will focus on absorption events with measurements as a special case. A helpful list of RTI terminology has been provided [7] and it will be adapted here to begin the structured argument. In a further adaptation I will seek to avoid mention of waves because pictures of wave propagation in empirical space have been a major source of confusion.
- micro-emitter: an excited quantum object with the propensity to release of quantum of energy (\(\hbar \omega\))
- micro-absorber: a quantum object with a propensity to be excited from a lower energy state to a higher one on receiving offered the quantum energy
- macro-emitter: a collection of \(N_E : N_E \gg1 \) micro-emitters
- macro-absorber: a collection of \(N_A : N_A \gg 1\) micro-absorbers
- emission: a micro-emitter generates an offer \(|\omega>\) of energy \(\hbar \omega\)
- absorber response: a micro-absorber generates a confirmation (\(<\omega , k|\))
- corresponding to the component of the offer received by it
- instantiating a non-unitary transition
- absorption: an actualised transaction in which conserved quantities (e.g. energy) are transferred from the emitter to a particular micro-absorber, resulting in excitation of the latter. This is irreversible (non-unitary) and random.
Setting aside the macro items for the moment, 1-2 indicate the elements in place to carry out a transaction. 5-7 is the transaction process resulting in absorption and a transfer of energy. The main part of the physics missing is the creation and annihilation of the boson that carries the quantum from the emitter to an absorber. In point 6 the presence of \(k\) was not explained. It has to do with the role of the photon.
The photon
Although we are now working with a physical ontology consisting of a quantum substrate and a supervening space-time of events, there is a strong intuitional pull towards thinking of photons as quantised elements of electromagnetic fields in space-time. In standard classical electrodynamics it is possible to construct free waves solutions of the homogeneous (source free) Maxwell equations. A commonly held physical intuition would picture these free waves as having some distant source but this source only has a role in the physics narrative and does not affect the future propagation and eventual interaction of the wave. There are also solutions to the inhomogeneous Maxwell equations that show how the propagating fields are created and there is a theory of wave interaction with matter (charges). In contrast the Wheeler-Feynman classical theory of electromagnetism places emission and absorption in centre stage and not only diminishes but eliminates the free field [2, 3].
Both forms of classical electrodynamics are now replaced with some form of Quantum Electrodynamics (QED). Standard quantum electrodynamics [e.g., 8] carries over some intuitions from standard classical electrodynamics. Quantisation produces two kinds of photon commonly known as real and virtual. The real photon corresponds to quantising the freely propagating classical wave. The virtual photon mediates interaction between moving charges. The virtual photon is created and destroyed with a finite lifetime as it mediates the interaction. This virtual photon is sometimes referred to as internal because of how it is portrayed in Feynman diagrammes, as shown below for the electron-electron interaction [8, Fig. 7-3]
Davies recognises this
virtual and
real terminology is confusing [5] in direct action quantum theory. I can only agree. Transactional quantum mechanics has taken strong guidance from the mechanisms of classical Wheeler-Feynmann electrodynamics. In clarifying the physics of the transaction RTI builds on the direct-action QED developed by Davies [4, 5]. It is a theory of photon exchange but with ontological ambiguity about the status of the photon. As indicated above, in the RTI the physical stratum of the ontology includes two interplaying layers: the quantum substrate (QS) and empirical space-time with its entities. To decide on which layer entities belong requires some analysis. In all mathematical physical theory, there are constructs that correspond to entities in the ontology and some that do not - they are useful conceptual scaffolding. Just as in standard quantum mechanics, there may be versions of RTI that gives ontological preference to a wave picture or one that gives preference to a statistical transition picture. Ruth Kastner's presentation makes use of a wave picture, with offer and confirmation waves. I am interested in seeing how far a
probabilistic transition picture can be developed. To help in this, rather than carrying over the "real" and "virtual" terminology from standard QED, it may be more productive to embrace fully the language of potentiality.
A quantum subsystem (QS entity) may have the
potential to emit a quantum of energy. For example, it may be a QS atom in an excited state. It may also have potential to do other things such as bond with another atom to form a molecule. How that potential may or may not be realised depends not only on the atom but its environment. In the QS we must not think about this environment in four-dimensional space-time terms. Here the generalised probability formulation of quantum mechanics may help. In this formulation the quantum sub-system of interest has potentialities that are conditioned on other entities in the QS. It is proposed that this conditioning is a QS physical effect and not just a mathematical manipulation in the theory. It is transactional. So, a quantum sub-system has a set of potentialities, and these potentialities form a complex that can separate into subsets of possibilities that have well defined probability spaces, in their mathematical description. Physically they are events that are conditioned to occur. Using a concept from Barbara Vetter's theory of
Potentiality, we have a two-step iterated potentiality:
- The potential possibilities that the sub-system could manifest are encapsulated within a complex (represented mathematically by the \(\sigma\)-complex)
- In the first step, the QS environment interacts with the sub-systems to realise sub-sets of statistical potentiality. This can be thought of as a step to propensity with statistical weightings realised through conditioning
- In the second step the possibilities of the statistical potentiality are sampled by the other entities in the QS, and this can, but need not, lead to a space-time event.
I have used the term "sampled" as it is familiar from statistics. It should be emphasised that this is not the observational sampling that statistical offices undertake or that a moderator may do by extracting a numbered ball from an urn in a lottery game. Here we have a physical active transactional sampling of one part of the QS by another. This can also be considered to be the physical interpretation of the role of projection operators associated with the sub-system's manifestation possibilities. This is an alternative to Ruth Kastner's
symmetry breaking explanation as to why only one of a set of possibilities is realised. More generally [6] a representation of the physics is formulated in terms of creation and annihilation operators for photons acting on a Fock space [8]. This in turn has a natural representation in terms of projection operators, as used in the adapted
Kochen re-formulation of standard quantum mechanics.
The rich mathematical structure describing the QS cannot be accommodated in four-dimensional space-time. This was recognised previously (*) but then usually neglected to concentrate on empirical and technological success. Or work with an otology restricted to "be-ables" in four-dimensions. The four-dimensional space-time does, however, seem to represent the empirical space where events take place and experiments are carried out. If empirical space supervenes on the quantum substrate, then to what extend does the QS determine the space-time structure?
The structural laws of space-time may emerge in the empirical space and not be determined in anyway by the structure and laws of the QS but this should not be assumed prior to investigation. For both standard QED and RTI quantum theory the space-time structures developed in relativity theory strongly influenced the mathematical form of the theories. So, the relativistic mathematical structure of space-time has been inserted, or pre-supposed, in constructing the theories. As we only have direct access to events at the empirical level it is inevitable that the space-time structures describing physics at that level inform the mathematical representation of the QS. However, it has transpired that while locally observed quantum events obey relativistic locality the statistical corelations between space separated events do not always do so. So, despite having used space-time relativistic structure to guide the construction of the mathematical representation of the QS, theory leads to predicted violation of relativistic principles at the empirical level. That is, robust statistical correlation is observed between space-like separated events. It is only through the construction of experiments based on the EPR "paradox", motivated by quantum theory, which has led to the confirmation of this effect.
What has been developed in RTI quantum theory is a theory of emission and absorption of photons that provides a mechanism for no-unitary system dynamics. However, more generally, other particles can be emitted and absorbed (or so it seems from second quantisation of standard quantum mechanics). For example, the electron dynamics also can be described using creation and annihilation operators acting on a Fock space. What we cannot do here is be guided by classical wave theory of emission and absorption of point particles - there is no such thing. Tackling these issues will need a deeper dive into the mathematical structure of the theory.
(*) Gentleman: there's
lots of room left in Hilbert Space. Sanders Mac Lane
References
- Ruth E. Kastner, The Transactional Interpretation of Quantum Mechanics - A Relativistic Treatment, Cambridge University Press, second edition 2022
- John A. Wheeler, Richard P. Feynman, (1945). Interaction with the Absorber as the Mechanism of Radiation. Reviews of Modern Physics. 17 (2–3): 157–181.
- John A. Wheeler, Richard P. Feynman, (1949). "Classical Electrodynamics in Terms of Direct Interparticle Action". Reviews of Modern Physics. 21 (3): 425–433.
- Paul C. W. Davies, (1971) Extension of Wheeler-Feynman Quantum Theory to the Relativistic Domain I. Scattering Processes, J. Phys. A: Gen. Phys. 4, 836.
- Paul C. W. Davies, (1972) Extension of Wheeler-Feynman Quantum Theory to the Relativistic Domain II. Emission Processes, J. Phys. A: Gen. Phys. 5, 1025-1036.
- Ruth E. Kastner, and John G. Cramer, (2018). Quantifying absorption in the Transactional Interpretation. International Journal of Quantum Foundations 4:3, 210–22.
- Ruth E. Kastner, (2018) On the status of the measurement problem: recalling the relativistic transactional interpretation. International Journal of Quantum Foundations 4:1, 128–41.
- James D. Bjorken and Sidney D. Drell, (1964) Relativistic Quantum Mechanics, McGraw-Hill Book Company

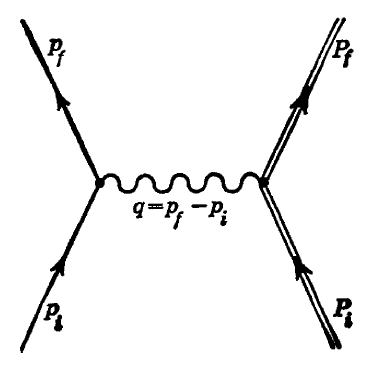
Ruth Kaster does have a theory (fermion) electron emission. It is mediated by photons. The electrons stay in the QS. I will return to this.
ReplyDeleteRe: "So, the relativistic mathematical structure of space-time has been inserted, or pre-supposed, in constructing the theories." In standard QED, yes. But this is not the case of RTI. The Lorentzian structure and Einstein's equations actually emerge naturally from the transactional picture, as laid out in my recent paper with Andreas Schaltter on what we may call "Transactional Entropic Gravity": https://iopscience.iop.org/article/10.1088/2399-6528/acd6d7
DeleteYes, thanks, I will have to work through this. Andreas Schaltter also seems to have done some interesting work that I will also investigate.
DeleteI have had time so far tp have a brief look at your paper and was interested to read "Another type of unitary process in the QS is the Schrödinger evolution of fermionic matter, such as electrons, or bound states such as atoms." So, the QS dynamics Galilean invariant on some 4-d space that is not empirical spacetime?
I am currently working through "The Ultimate Constituents of the Material World: In Search of an Ontology for Fundamental Physics" by Meinard Kuhlmann. It's not RTI but his thinking on a dispositional ontology may be useful.
Thanks, I have republished your comment. It was there when I posted my reply.
DeleteThanks!
Delete